数据满足正态分布是进行很多统计分析的前提,如果不符合正态分布,则需要对数据进行转换。常用的转化方式有:
- 取根号
- 取对数
- 取倒数
今天我们看一看什么条件下应该选用合适的转换方式。
# 生成正态分布数据
normal <- rnorm(100,mean = 5, sd = 2.5)
plot(normal)
# 从直方图可以看出数据符合正态分布
hist(normal)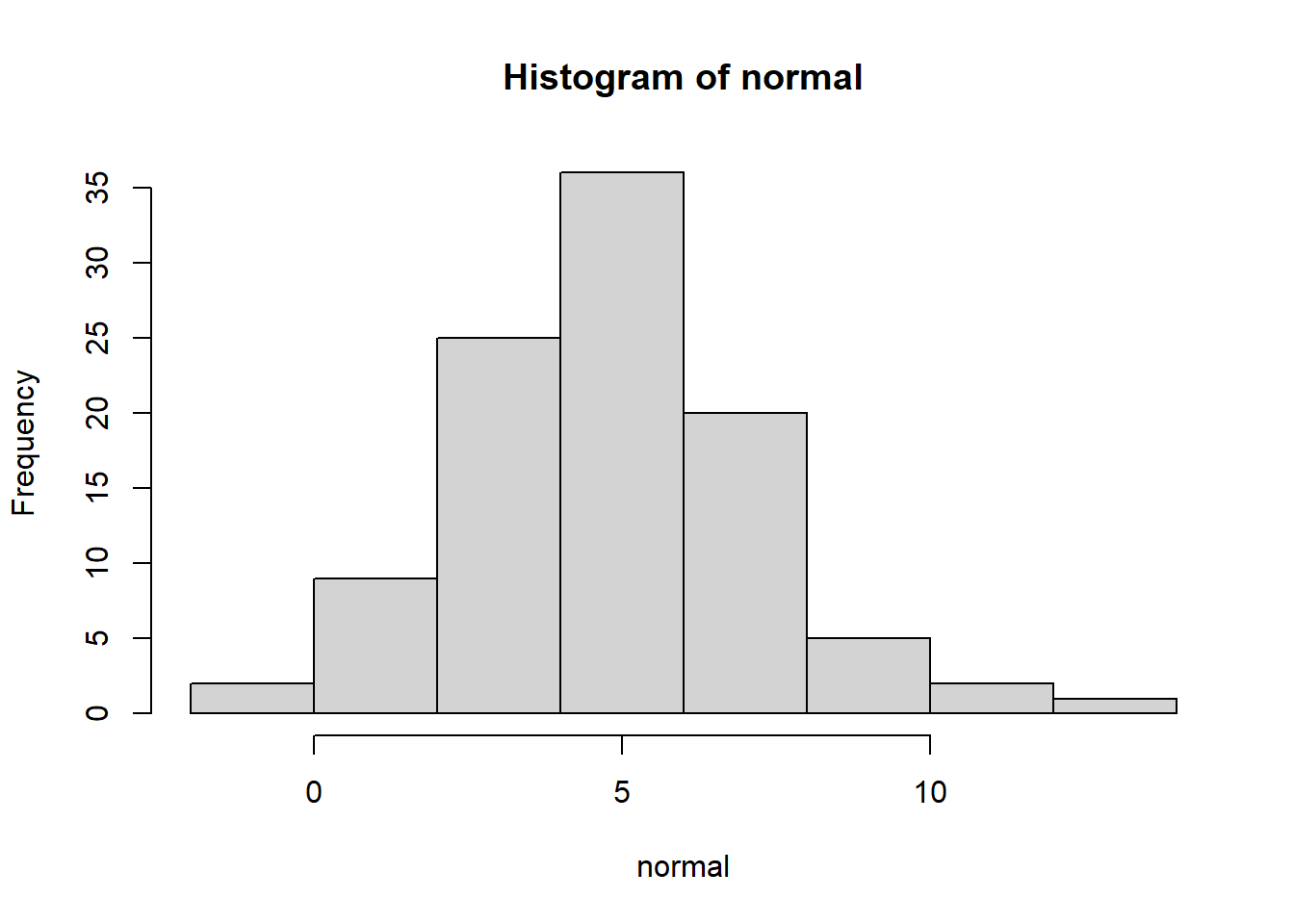
# 从QQ plot也可以看出来
qqnorm(normal)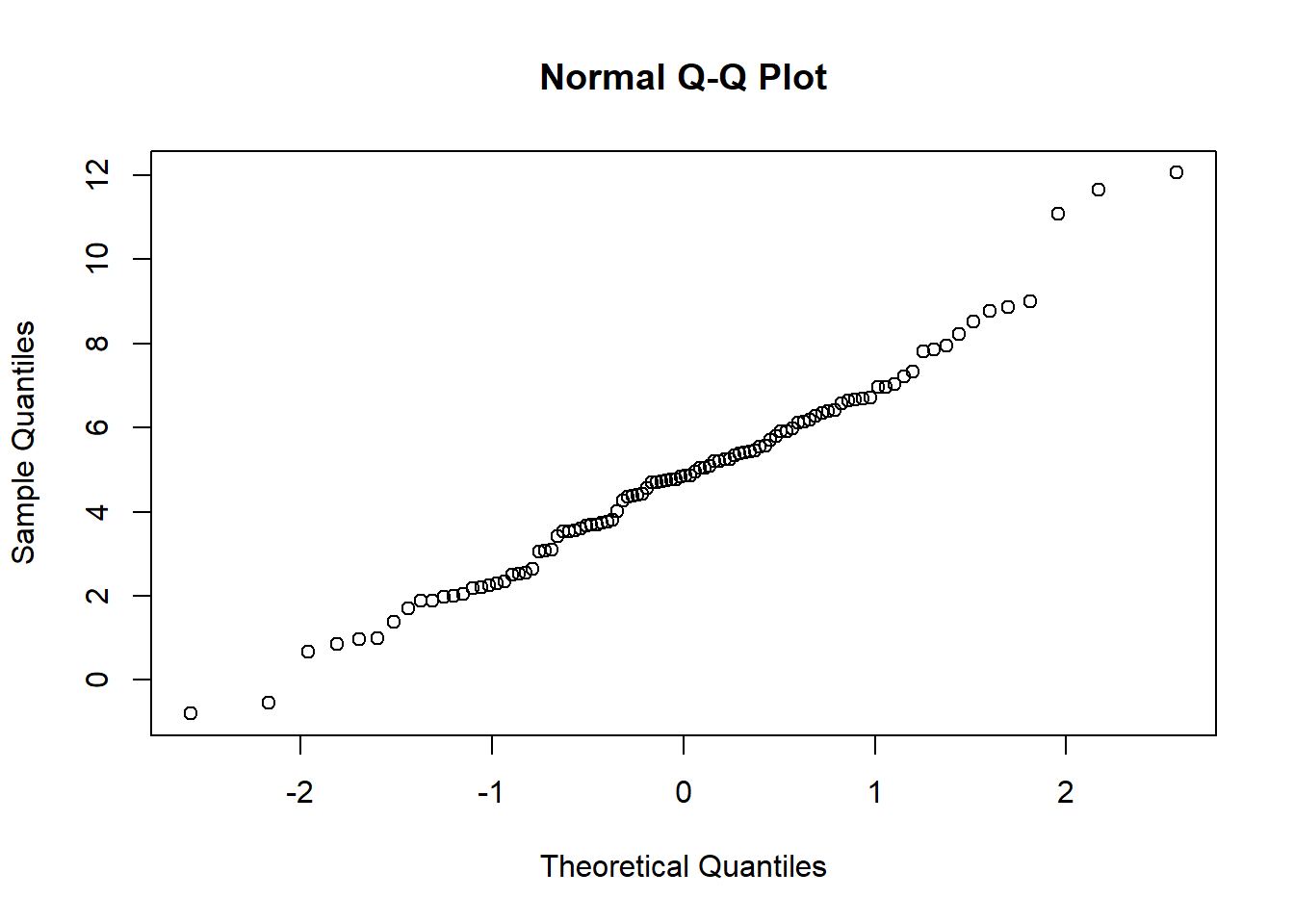
对正态数据进行平方运算后,直方图显示数据成了左偏的结构。反过来,意味着如果你正在使用的数据与下面的数据分布类似,则可以尝试用开平方的方法来做数据标准化。
# 数据的平方根
normal_square <- normal ^ 2
# 现在的直方图
hist(normal_square)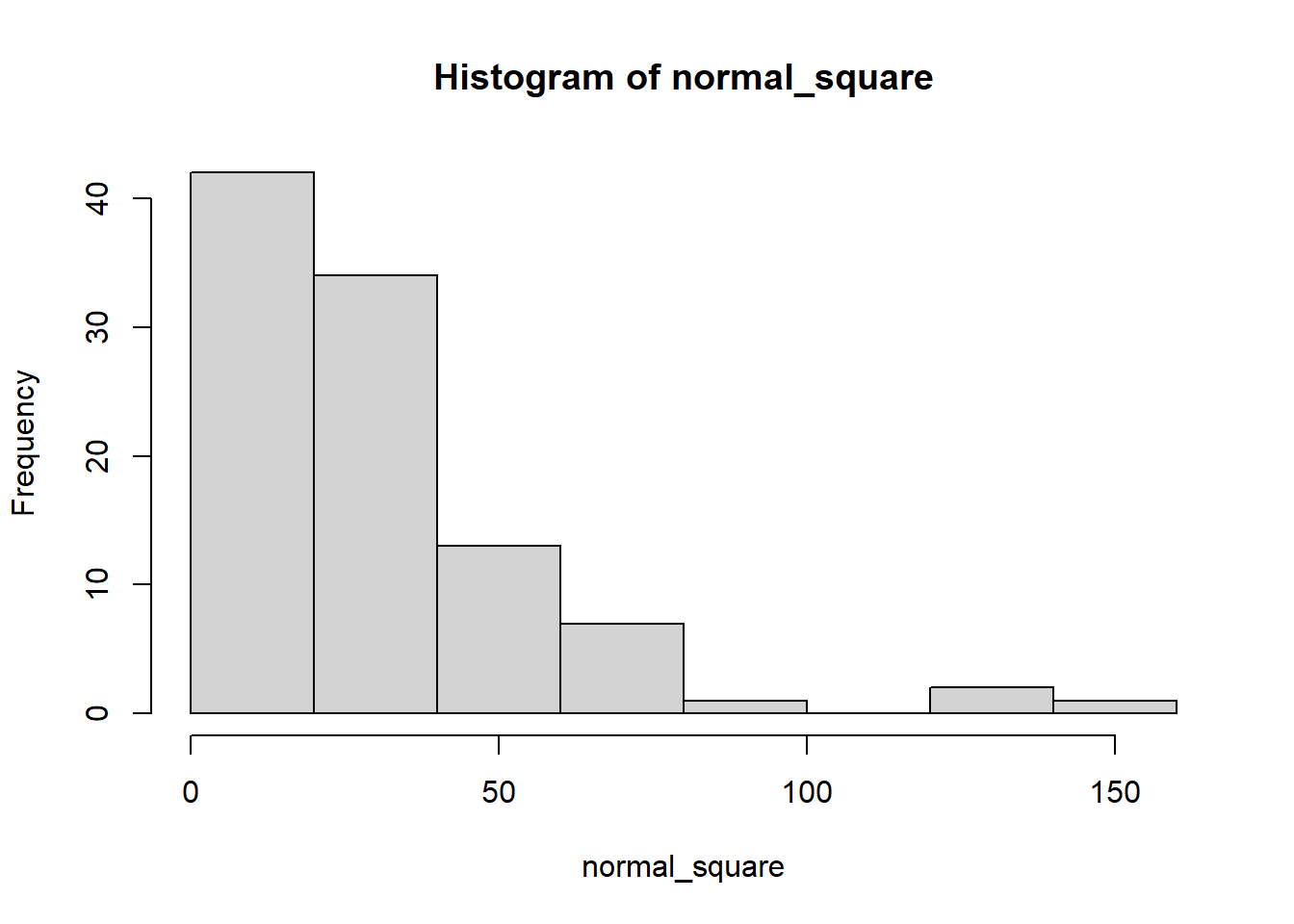
对正态数据进行幂值运算后,数值也是一个左偏的分布,但与平方计算的结构有所不同。
# 数据的幂值
normal_exp <- exp(normal)
hist(normal_exp)
对正态数据进行倒数运算后,数值是一个中间翘起来的分布。
# 数据的幂值
normal_reciprocal <- 1/normal
hist(normal_reciprocal)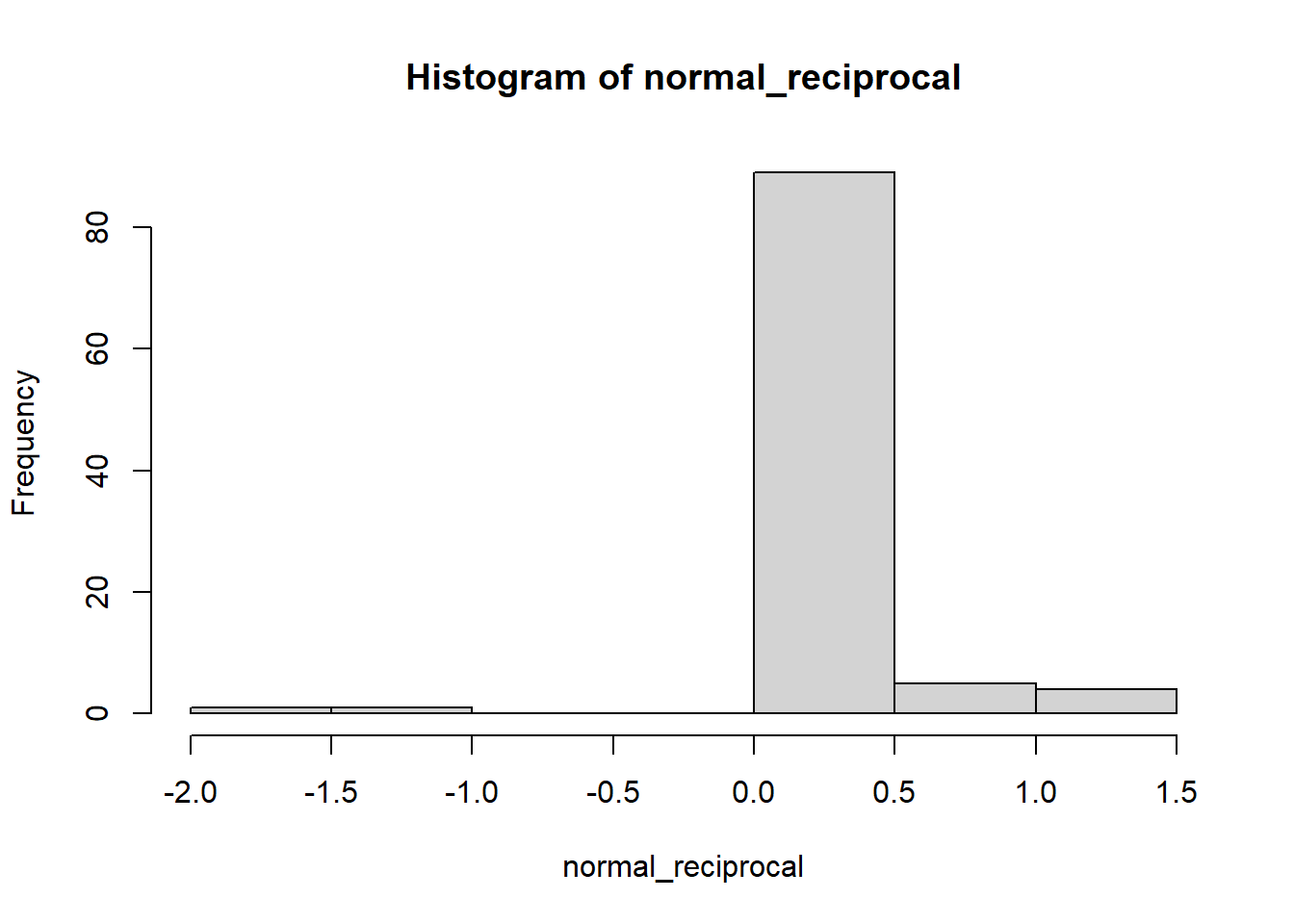
上述3种方法转换正态分布后,都是正偏态数据(偏度Skewness > 0 )。
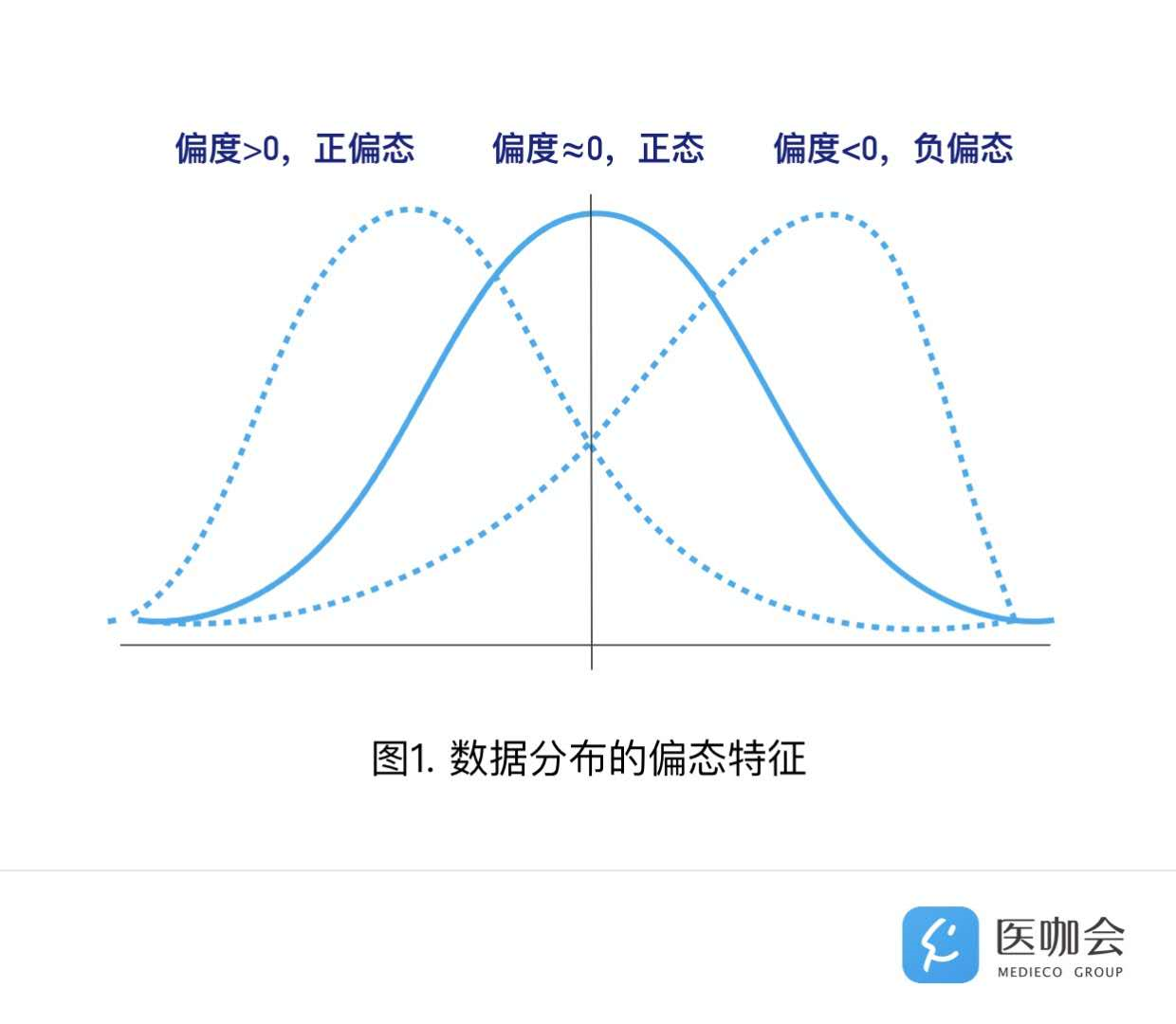
如果是负偏态数据,则需要将负偏态资料进行反转,转换为正偏态,然后再参考正偏态分布资料的转换方法进行转换。
反转的方法:首先找出该数据系列的最大值max,用max+1,在减去每个数值。
接下来也用反向转换的方式,看看负偏态数据的分布规律吧。
# 轻度负偏态
normal_square_rev <- max(normal_square)+1-normal_square
hist(normal_square_rev)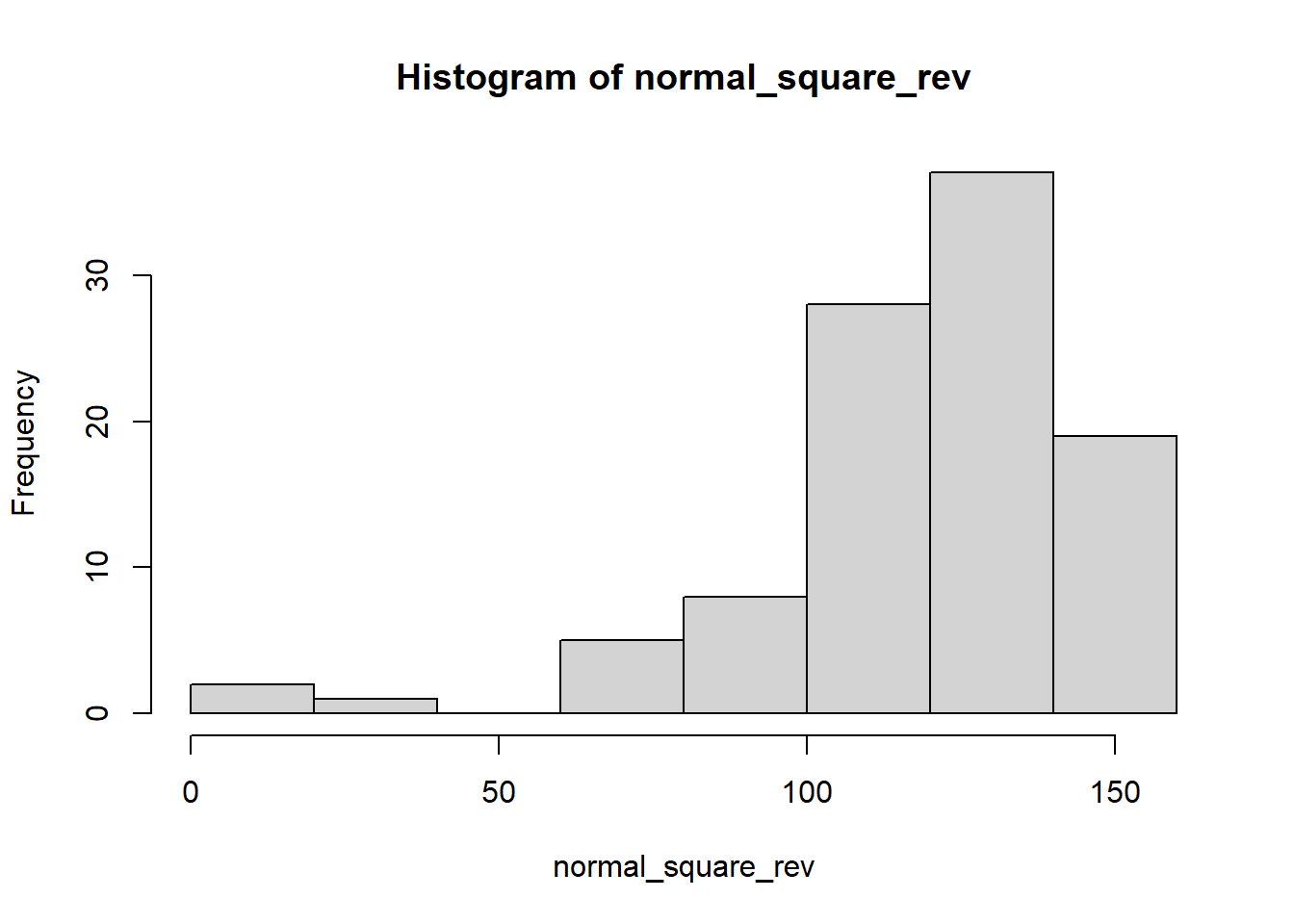
# 中度负偏态
normal_exp_rev <- max(normal_exp)+1-normal_exp
hist(normal_exp_rev)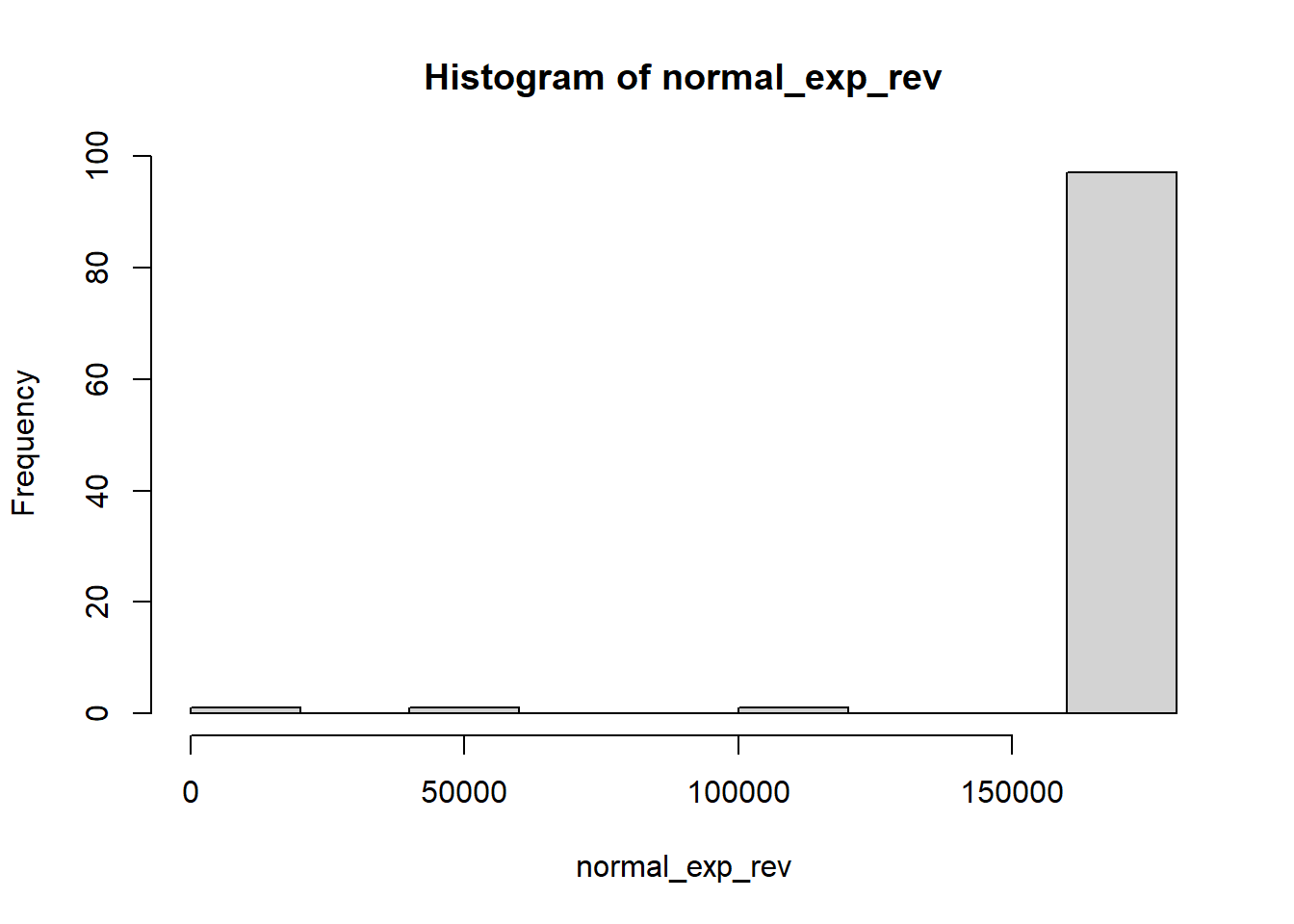
# 重度负偏态
normal_reciprocal_rev <- max(normal_reciprocal) + 1 - normal_reciprocal
hist(normal_reciprocal_rev)
注意事项:
- 不是任何非正态数据都可以进行正态转换;
- 如果比较两组数据时对一组进行了正态转换,另一组也应做对应转换;
- 在进行相关分析或线性回归时,要求变量间存在线性关系,如果因变量与某个自变量之间呈现出曲线趋势,此时转换的变量可以是自变量,也可以是因变量,或者两者均可。如果进行了变量变换,则应当重新绘制散点图,以保证线性趋势在变换后仍然存在。
- 在对线性回归模型进行解释时,如果使用函数转换的方法对变量进行了转换,则解释时应按照转换后的变量给予解释,或者可以根据转换时使用的函数关系,倒推原始自变量对原始因变量的效应大小。
另外,在判定数据是否符合正态分布的时候,会用到检验和QQ图、直方图等方法。一些检验方法经常会得出数据不满足正态分布的结果,但事实上只要在图形上显现出正态规律,一般还是可以认为数据来源于一个正态总体。
事实上,Shapiro-Wilk检验及Kolmogorov-Smirnov检验从实用性的角度,远不如图形工具进行直观判断好用。在使用这两种检验方法的时候要注意,当样本量较少的时候,检验结果不够敏感,即使数据分布有一定的偏离也不一定能检验出来;而当样本量较大的时候,检验结果又会太过敏感,只要数据稍微有一点偏离,P值就会<0.05,检验结果倾向于拒绝原假设,认为数据不服从正态分布。所以,如果样本量足够多,即使检验结果P<0.05,数据来自的总体也可能是服从正态分布的。
因此,在实际的应用中,往往会出现这样的情况,明明直方图显示分布很对称,但正态性检验的结果P值却<0.05,拒绝原假设认为不服从正态分布。此时建议大家不要太刻意追求正态性检验的P值,一定要参考直方图、P-P图等图形工具来帮助判断。很多统计学方法,如T检验、方差分析等,与其说要求数据严格服从正态分布,不如说“数据分布不要过于偏态”更为合适。